This is mathematical section of the parent essay Gödel Incompleteness for Startups

Gödel Numbering

A formal system is just a collection of axioms and rules. Just like we did before we can record axioms in plain English like “Number 0 exists”.

Can we associate axioms and rules with natural numbers? As you know everything you read on computer, is actually encoded into numbers. Inside the computer letter “N” is 78, letter “u” is 117, etc. What is word “Number” for us, is just 7811710998101114 for the computer – just one long number.  Why is it that “N” is 78 and not 87, or 8787? No reason, its arbitrary arrangement, called encoding standard. That specific standard called ASCII which states that all computers who want to be ASCII-compatible must assign “N” to 78 and vise versa.

But here is an interesting part, a key to Gödel’s proof: Our axiom “Number 0 exists” is first axiom in a system that defines existence of numbers and simple arithmetic. At same time we can encode “Number 0 exists” using ASCII encoding, or any other encoding we choose and get a number that represents that axiom (or a rule) about numbers themselves. You will get something like the following:

• Number 0 exists ⇔ 7811710998101114324832101120105115116115
• Each number has a successor that is a number ⇔ 6997991043211011710998101114321049711532973211511 7999910111511511111432116104971163210511532973211 011710998101114

That number is awfully long, yet it’s still just a number. And then we do the same for rest of your initial axioms and rules. Then you can start encoding your first deductions about the formal system, deductions of deductions, etc. In the end any axiom or sequence of deductions will be just a long arithmetical number.

Something interesting happens here. On one hand we define a formal system that describes basic properties of natural numbers. On the other hand because of the encoding these very axioms and rules are also numbers themselves! We can go back and forth as we want. We can deal with axioms as plain English text. Or we can switch them into pure, even if very long, numbers, and deal with them as just a set of numbers. The system becomes self-referential: axioms and rules describe what numbers are and at same time are just numbers themselves.

In reality English is very long and inefficient way to describe formal systems. Logicians developed much more compact syntax to describe such systems. Also, ASCII encoding is good for computers, but it lacks certain properties critical for Gödel’s proof. Gödel come up with his own totally unique encoding, which is called Gödel-numbering. Remarkably, he came up with such numbering decades before computers or anything like ASCII existed. That encoding uses prime numbers, which thanks to absolutely fundamental Prime Factorization Theorem gives such encoding important properties that are critical for next steps of the proof. That type of encoding ensures that each unique sequence of logical symbols – axioms, rules, and deductions – have one and only one unique Gödel-number. And one can always move back and forth between Gödel-numbers and original sequences of symbols that originated them¹.

Now we can write down logical statements of any length using standard symbols of logic, and then convert them to Gödel numbers. We describe the axioms and rules of formal system about natural numbers (or more complex formal system) and thanks to the magic of Gödel numbering these statements at same time will be just big natural numbers. From the shortest axiom to complicated long chains of deductions that may end up stating something like “User acquisition campaign will have positive arbitrage if lifetime value of average user is higher then average user acquisition cost” – everything in the end can be associated with just a number. And we can deal with these numbers like regular math: prove theorems about them, and show which properties and relationships with each other they have like all numbers do.

Instead of dealing with very complicated matters of the infinite number of all possible proofs within given logical system, Gödel effectively is saying to us:

You know, we don’t have to deal with all that insane complexity. Let me show you a unique way how any proof can become just a big number, and how any such number can be converted back to exactly same proof. Any proof you produce, be that a 10 page proof or 1000 page proof, is just one unique number fully representing your proof. And that’s true for all and any possible proofs. From now on, we can just deal and prove theorems about numbers and functions of numbers. That is a much simpler task.

 I Can Prove It

What Gödel does next would be familiar to modern software developer – never mind that he did it many decades before such concepts entered our technical lexicon. He would develop his own personal library of functions, in fact almost a domain-specific language required to solve the problem he set out to solve. And as mere side effect he invents modern recursion. Speaking again in modern terms he diligently proves that all functions he constructs are computable – that they can deliver specific answer in finite (even if may be large) number of discrete steps. The hints of future Turing Machine are floating in the air of his definition of primitive recursion.

The first function is almost trivial: he defines what it means “x is divisible by y”. In modern logical language it would be written down as

1. y | x ⇔ ∃z ≤ x . x = y ∙ z

In plain English says “x is divisible by y if there exists such z that is smaller or equal to x and x is equal to that z multiplied by y” Well, that makes sense: that’s exactly is definition of division.

Afterward definitions start to make use of previous ones like a function calls of modern software library. That allows Gödel to quickly build up complexity of his deductions. Next he defines what is prime number:

2. isPrime(x) ⇔ ￢(∃z ≤ x . ( z≠1 ⋀ z≠x ⋀ z|x)) ⋀ (x>1)

As you can see logical syntax allow you to make more complicated deductions if you follow the rules of the system to create longer statements. That particular statement says “x is a prime number if there are no such number z that is smaller then x, where z is not 1, nor z is equal to x and x is divisible by z. Also x must be larger then 1”. That’s just very explicit statement that x is divisible only by itself or by 1. There is no other numbers that x is divisible by – which is definition of a prime number.

And so on Gödel continues to build logical scaffolding of his library. Starting from Peano axioms he keeps deducing more and more elaborate functions. What is the purpose of that library he is building? Gödel goal is ingenious: he actually wants to describe a function that checks what is provable, what is correct deduction in any logical system.

Gödel-numbering allows us to encode the syntax of logical statements. However that tells us nothing about content of such statements. I can say “For any x it’s always x+1=5” which obviously is completely wrong  (false for all values of x other then 4) yet nonetheless I can easily write it down. Logical syntax allows us to write down any sort of statement – incomplete, meaningless and false – as well as few statements that are actually true provable deductions of the system. How to differentiate between nonsensical statements and actual proofs?

When I was writing that wrong statement above, I had broken certain rules of deduction in our logical system. To be a real proof I need to start from axioms, build immediate consequence of these axioms, and finally after correct use of all rules of inherence arrive at whatever statement I’m trying to prove. True proof cannot be just written down as lone statement. It’s always a strict sequence going all way back to initial axioms of the system. Turns out all the steps to verify that specific sequence is a real correct proof can be checked and verified by purely mathematical function! With no less then 45 intermediate results Gödel arrives at that function number 46: provable(x)²

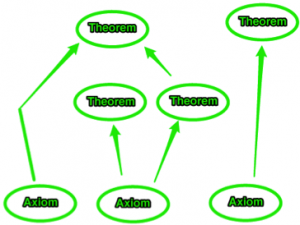provable(x) is similar to an English teacher grading papers. When writing in English (just like in logical syntax) you can write any sort of nonsense, texts full of misspellings and grammatical mistakes – A Good teacher will have none of it. Well-written texts will get passing grades, while texts with nonsense or mistakes will be rejected. provable(x) does the same for proofs written in syntax of logic. If “x” is correct sequence of logical deductions, in which all axioms and rules are properly followed, provable(x) will confirm that such (x) is a valid proof. If x is instead nonsense or a wrong proof it will get rejected. Obviously provable(x) relies heavily on every single other function Gödel defined in steps 1 to 45. It is a massive amount of work of mind-bending complexity. Yet all that complexity is expressed and encoded in pure symbols of mathematical logic.

The self-referential nature of any logical system is becoming exposed again. From pure mathematical perspective provable(x) is just a function like any other. Its certainly a very complicated function, yet beside the requirement of doing many complicated steps to arrive at the result there is nothing “magical” about it on the surface. It takes one argument and returns certain result. It’s like any other function you can find in a math reference book. Yet at same time the purpose of that one function is certainly “magical” for the formal system it belongs to. That very formula describes what can and cannot be proven in that very system.  That function gives the system a voice, and system starts to speak about itself to tells us what is possible inside it. Things certainly are getting “curiouser” and “curiouser”.

Einstein, Gödel & The Constitution of the United States

Like many of us in Silicon Valley Gödel was an immigrant and had to prepare for a citizenship test. Naturally when this mastermind of logic started to study the Constitution of the United States it wasn’t long before he spotted a problem.  According to Gödel, he found an inconsistency in the Constitution that would allow democracy to deteriorate to the tyranny. Gödel’s friends, knowing full well that no social protocol would ever stop Gödel from speaking against perceived logical violations, decided to dispatch handlers to make sure Gödel actually passes his citizenship exam. One of the handlers was Albert Einstein himself. Despite handlers best effort to distract Gödel he still managed to present his findings to the judge officiating the ceremony. Thankfully it was the same judge who administered the oath to Einstein few years earlier and Gödel passed his exam without an incident. Not bad having Einstein as your sidekick when you decide to tell the judge you had found a logical error in nation’s ultimate legal document!

Diagonal Lemma

Here is unavoidable yet very simple math. Diagonal lemma wasn’t initially part of the proof; using his sheer brainpower Gödel just implicitly worked it out inside his overall proof.  The lemma states that in given system of Gödel-numbering there always will be at least one number f for any logical formula F that f = Gödel-Number (F(f)).

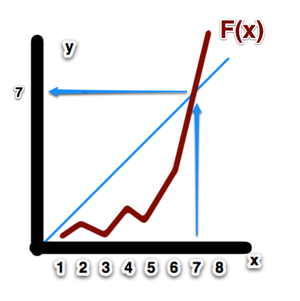Intuitively such proof can be grasped that if we start graphing such y=Gödel-Number (F(x)) on a piece of paper starting from x=0, x=1, x=2 and putting dots where we get corresponding G-numbers. We keep increasing x and keep moving along the axis to the right. The lemma proves that sooner or later that graph will intersect the diagonal where y=x. Therefore³ we get at least one number that remains itself when it passes through function F and result is converted to final G-number.

The Proof

Now Gödel has all pieces of puzzle together to bring biggest surprise in history of mathematics. The “Theorem VI” in his paper is very complicated. Here is the sketch proof that is traditionally used to describe its key finding.

As we discussed provable(x) is designed in many complicated steps to be a function that checks if x is provable statement. We can define another function, NP(x) = NOT provable(x). “NOT” is simple operation of logic. It reverses what’s given to it. provable(x) can be only true or false – either x is the proof or it is not. “NOT” will reverse true to false and vice versa. Since NP(x) is also a function of a single number we can use diagonal lemma on that particular function. Thus there must exist such number g such that g = Gödel-Number (NP(g)). So far it’s pretty straightforward. We plot NP(x) as a function, find where it will intersect diagonal line of its y|x plot, and mark the number g of that intersection.

Lets construct a logical statement G = NOT provable(g). In this case G is no longer a function – since we plugged in specific number g –now it’s just very long logical expression expanded according to the complicated logical syntax contents of provable(x) – where our specific number g takes place of free variable x. Is that specific logical statement true and can it be proven?

Lets think about this for a moment. provable(x) is designed so that it can tell us “true” or “false” about any given x. Therefore NOT provable(x) can only be true or false as well. Now we take that specific number g and need to figure out what would be G = NOT provable(g) evaluates to? There are only two answers: true or false, which one it’s going to be?

G is false

Lets consider what happens if G is false. Well, we defined G as “NOT provable(g)”. If G is false, then provable(g) is true. Because we used diagonal lemma to figure out value of number g, we know that g = Gödel-Number(NP(g)) = Gödel-Number(G). That means that provable(g)=true describes proof “encoded” in Gödel-Number g and that proof is correct! We got correct proof g of false statement G. Ka-boom! The whole consistency of our system just went down in big nuclear explosion: we got specific proof of G that actually is a false statement! Your system just became inconsistent: you can prove a false statement, meaning you can prove anything and everything. Not good. Not good at all.

G is true

Ok, so making G false is not a good move, which immediately leads to an inconsistent system. Then lets consider what happens if G is true. We obviously would prefer our system to remain consistent – otherwise it utterly useless – so our only option left is to assume G is true. Back to definition G=NOT provable(g). If G is true, then provable(g) is false. Our strict logical bookkeeper that lives inside provable(x) tells us “g doesn’t not contain any sequence I would accept as valid proof. Among all possible proofs you can encode in your system, g is just not one of them”. Therefore there is no such sequence of logical deductions; there is no text that can be put on paper that will prove G.

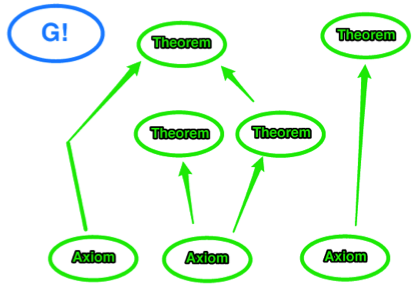G is true. And at same time there is no proof of G. G is unprovable in our logical system. If proofs are villages in big network of roads, then all roads leading from our initial axioms will never arrive at G. G exits and its apparently true – yet there is just no logical road on our map that will start at axioms and arrive to the point G. All deductions you can make about your system wont include G, so your system will be incomplete.

And that’s exactly what Gödel is telling you: “Any … formal system capable of expressing elementary arithmetic cannot be both consistent and complete”

If you want to keep consistency of your system you will have to accept there are such G-statements that are true yet unprovable in your system – your system will always be incomplete. Or you can insist on making them provable, which will immediately make such system inconsistent.  You can take one or the other, but you cannot have both at same time for any formal system rich enough to express simplest axioms of arithmetic⁴.

There is something very amazing about Gödel proof. We used to think about logical systems as dry and boring sequence of strange symbols written on paper. Yet suddenly it’s as if these symbols got a life of their own. As if the system itself got intelligence and started to describe to us what is its own axiom, what is the correct deduction of a theorem, what is provable statement. And finally the mind-bending G-statement is constructed showing there are true statements that can be written down … yet they will never be proven inside that system. The truth is out there… and totally out of your reach!

How much of that hidden knowledge is out there? Apparently an infinity. Here is why. Gödel made his proof even harder then necessary because he wanted to demonstrate one interesting consequence. What if we add G as a new axiom to our system? After all we know its true, since otherwise the system would be inconsistent. Would it make our system complete? It turns out that adding a new axiom to the system, changes the system! Remember all the steps to define provable(x) ? Since now we added new axiom to list of all original axioms, we would need to retrace our steps we took in defining provable(x) to account for the new axiom we just added. So now we are dealing with a new system, in which it will be new function provable’(x) that in turn will create new statement G’. And G’ is a different statement then the first G we already added as an axiom. So now you have a second unprovable statement for an expanded system. You can repeat same process to get G’’, then G’’’ and get an infinity of true yet unprovable statements for a sequence of ever expanding formal systems.

If some of you are totally confused at that point, I wont blame you. G-statement is a highly abstract construct. So all formal systems are incomplete, but how can we practically use that fact? For all its unrivaled mathematical brilliance Gödel’s proof leaves us pretty much where we started.

Before making our own deductions about real world applications, let’s actually build out more insights about that strange world of formal systems. Just like billiard balls hitting each other at an angle to go into different directions, to understand the full implications of Gödel’s result lets review a few other important mathematical results closely related to his work. The first of these is Turing’s Halting Problem.

Halting Problem

Turning’s famous Halting Problem is well known by software developers. In simple language Halting Problem states the following:

Let suppose I will give you the source code of a computer program. I will also give you all the data used by that program, files, hard drives or DVDs it will process. Can you tell me if that program will eventually print some sort of results we expect it to produce and HALT having accomplished its job, or it will run forever unable to finish it? In other words by looking at program and its data can you give me quick “yes/no” answer will it ever stop?

Turing had proven decisively that Halting Problem is impossible to solve.  It’s impossible to write software that will take a look at source code of another program and make a determination if such program will ever stop running (halt) or will be running forever. It’s a restatement of Gödel proof for more specific domain of software. The proof is largely the same as Godel’s just easier to grasp it can be formulated as simple software code rather then mind-bending functions operating on syntax of logic⁵. Halting’s Problem proof is very easy to understand for software developers and not very useful for everyone else so we will not cover it here unless you want to read it on your own.

Instead of providing a dry proof, lets demonstrate it with a practical example. Say I ask you to give me your prediction: will such program ever halt and stop working?

Start at x=4. Get me first prime number p that is less then x. Check if x-p is prime number too. If yes, increase x by 2 and repeat. If not, make p the next smaller prime and check again. Repeat that until you check for p=2. If x-p is still not prime number,print out x and then HALT 

This description is not very complicated and would be trivial in any modern computer language. Assuming we do not know the Halting Problem it would be tempting to think such a simple program would be certainly easy to predict.

The trick here is that I did not specify just any random program. The statements above describe famous Goldbach’s conjecture that have been utterly impossible to prove for almost 300 years. The software above just checks if the statement “Every even integer greater than 2 can be expressed as the sum of two primes” is true, and then moves on to the next even integer. The conjecture is totally true for all first 4 000 000 000 000 000 000 numbers checked so far, yet what we don’t have is hard mathematical proof.

The key insight here is that knowing if these few simple lines of computer code will ever halt is equivalent to having proof of Goldbach’s conjecture! If the conjecture is true the software will never halt, it will check all numbers to the infinity, never finding one that breaks the rule. If conjecture is wrong then software will stop as soon as it finds the first number that breaks the rule.

Something very interesting is going on. Software obviously is just another way to write down syntax of logical formal systems. We could use English or software code or even go low level with pure Gödel-style logical operators if we wish. Yet fundamentally in just few lines we can write down a statement that represents one of most fundamental problem of mathematics. Knowing when such program will halt – gives us the result we want to know – is the same as having proof of that incredibly hard problem. We can even rewrite the software above as Gödel recursive function and make a statement “will it be true that such function will halt on at least one number?” Yet again proving that statement is the same as proving Goldbach’s conjecture.

Goldbach’s conjecture is currently considered one of the big unsolved problems in math. Maybe someday someone will actually find the proof; but it is just as likely someone will prove that conjecture is undecidable without additional axioms. Such proofs are incredibly hard, yet such things  have been proven before.

Even the simplest expressions in a formal systems, such as a few lines of software code, can represent incredibly hard statements, some of which will be un-decidable with all our current mathematical knowledge. Software cannot be “bound” by another software. Software is so universal⁶ that its behavior can be totally unpredictable. Another piece of software can not tell you “in advance” what’s going to be the result. The only way to obtain the result is to run original software for as long as needed  – it could be a few hours till “halt”, or it might be an infinity of time.

The Halting problem shows the other side of the same coin. If a statement is un-decidable you cannot “cheat”, and just write software that will test that statement for you. Software can easily express that statement, but it might take infinite time for that software to finish working. And as long as you don’t have the proof of the statement neither can you prove if such software will ever stop working. There is infinitely more knowledge out there, more proofs: yet all this knowledge is unreachable to you as long as you are bound by the limits of your current system.

Since we are dealing with infinities now, its time to understand them better. Almost 40 years before Gödel made his entrance, another brilliant mind was analyzing first problems related to infinity.

The First Look At Infinity

When we think about infinity, the first thing that comes to mind is infinity of numbers. Yet it turns out that infinity is much more interesting that a simple every increasing row of numbers. Lets look at difference between natural numbers and real numbers. As we know natural numbers are simple numbers like 1, 2, 3 etc. that we use to count things. Real numbers are what we use to measure elements of the real world—i.e., the distance between two points is 1.23 miles. There is obviously an infinity of natural numbers like 1, 2, 3, 4, 5 and as obviously there is an infinity of real numbers like 1.23, 2.345, 3.123 etc.

Georg Cantor proved astonishing result – called Cantor’s Diagonal proof – even when using an infinite number of natural numbers you still can not count even infinite number of real numbers! Somehow infinity of natural numbers is just not “infinite” enough! There are different types of infinities; Infinity consisting of real numbers is more “powerful” then an infinity consisting of simple natural numbers. The proof is actually surprisingly simple.

1	⇔	1.1000…
2	⇔	1.2000…
3	⇔	1.3000…
…
10	⇔	1.01000…
11	⇔	1.11000…
12	⇔	1.21000
… later in the sequence …
123	⇔	1.321000…
… much later in the sequence …
12345678910	⇔	1.01987654321
… infinity later …
Infinitely long row of 9	⇔	1.999…(infinite 9)

Lets pretend the truth is actually the opposite: that we in fact can count all the real numbers. Lets start with counting all real numbers between 1 and 2. To make matters even simpler, we will count just by moving the increasing natural number to the right after “1.” and reversing the order of natural number digits⁷. You will get something like table on the left.

Whew, we are done. That table is obviously infinitely long, but now we used 100% of all natural numbers and got a corresponding real number. Now, did we actually count all the real numbers just between 1 and 2?

Lets construct the following number: we will go along the diagonal of our table and construct a number where each digit is +1 higher then what we see in the table. If digit to increase is 9 we will make it 0. I will mark the diagonal digit in color and and then we pick each digit and increase it by 1:

1	⇔	1.1000…
2	⇔	1.2000…
3	⇔	1.3000…
4	⇔	1.4000…
5	⇔	1.50000…
…

New Real Number = 1.211… (infinitely more digits)

So do we already have that “new number” in our table, is that a duplicate? Obviously not – since we specifically constructed it to be different in at least one digit from every single line in the table. This number doesn’t match any of our real numbers directly associated with natural numbers. But the table is natural-numbers-infinity long! We are out of natural numbers at this point – every natural number we could use is already in the table and associated with certain real number. We just constructed a new real number and have no space (among natural numbers) to associate it with.

Let me offer another example, which might help you grasp why infinity of real numbers, is called “continuum” it is so much more dense and powerful then infinity of countable numbers. Pick any two numbers you think are very close, much closer then our example of range from 1 to 2.

Lets pick 1.001 and 1.002. We made the range 1000 times smaller. Or we could have made it million times smaller. Then repeat the argument above trying to count all the real numbers in between. Obviously you would start with 1.0011, then 1.0012, 1.0013, etc. Your final number will be 1.001999…(infinity of 9), which actually rounds up to 1.002. So have you counted all the real numbers between 1.001 and 1.002? And you can repeat same diagonal argument to construct a new number between 1.001 and 1.002 that was not counted since it differs in at least one digit from all other numbers. Apparently even tiny segments between two real numbers have “more” infinity between them then all the infinity of natural numbers!

Apparently continuum infinity is very powerful. That’s the infinity that belongs to the real world around us – everything in our world is described by a real number. Yet we never know any of these real numbers exactly right. We are always limited by error of our instruments. At certain point our measuring tools will round up the result, and infinite sequence of digits of real number will be truncated. If you measuring distances with say tunneling microscope, you will round up the measurement to the nearest atom size. Such precision may create an illusion the world is fully measurable using scientific instruments. That is not true: rounded up final measurement no matter how precise, even if it’s to the limit of atomic sizes, is just simpler rational number. These rational numbers are countable with our familiar infinity of natural numbers. Yet the real world remains a continuum infinity never fully reachable to our tools.

That concludes our mathematical session. Now lets apply that hard earned knowledge to practical matters of startups & innovation. Lets return to our main essay.

---