Every year a few thousand startups are incubated in Silicon Valley. Few of them will succeed; the rest will decay or outright fail. Yet there always seems to be room for one more billion-dollar company. Besides appearing seemingly out of nowhere, the most radically successful startups are also the most unpredictable ones. What force seems to create these massive sources of wealth that initially look like “bad ideas” to everybody beside their founders?

You may be tempted to say “Black Swan,” and you would be correct; however, beside simple acceptance of extraordinarily rare random events, there is deeper mathematical influence over a process that constantly spawns new opportunities. Understanding that influence will help any startup founder or investor to improve his business insights. To understand these concepts better we will make a long journey that will touch upon very foundations of logic and mathematics .

I usually find time to look at about two hundred startups every year. Referrals arrive from other investors, startup founders I mentor or via the massive firehose of demo days at YCombinator & 500 Startups. As you can imagine, this creates an overwhelming supply of startups and innovative ideas to look into. Every startup presents the ultimate question: Is it worth it to invest your time and money? Or is it a waste of both? There is never enough time to dig deep enough into any single startup to understand it fully. Making an investment is not an easy or obvious decision. Yet, over the years, I started to notice certain meta-patterns common to all startups, the patterns that give a tantalizing premonitions on their chances of success or failure. The specifics of an industry or investment cycle might change, yet these patterns remain the same in every decade. I see them as two big groups of patterns: human patterns and mathematical patterns.

Human patterns emerge from our personal traits. Weather a startup will overcome its human-related challenge is determined by what a person or a team can succeed or fail at. The telltale sign is when the outcome will be determined by quality or quantity of personal efforts. What you typically read in Silicon Valley startup blogs would be all about such human patterns. It will be hundreds of topics covering which software language to use, how to pick founders, how to operate the company, how to build a product, how to build software, what is company culture etc. It’s all good content, yet it only addresses patterns driven by human traits, and thus is only half of the equation.

What you rarely hear about is “mathematical” patterns. These patterns emerge from objective nature of the reality where a startup must operate. The market dynamics, the ecosystem of industries they find themselves in, the governing trends of technological progress. As soon as a startup starts operating in the real world, the vast majority of factors will be outside of a startup direct control or even influence, while having absolutely dominating impact on that startup eventual outcome. Beside now legendary Black Swan¹ making big waves since 2006, there is almost no information on the mathematical fundamentals of startup formation and investing. Usually all you get is a non-actionable statement like “90% of all startups fail” after which the author promptly moves back to human factors, which are much easier to understand and analyze.

To help develop our mathematical intuition we will turn to one of the most profound mathematical results, provided by the legendary Kurt Gödel: The First Incompleteness Theorem. To most it is a seemingly dry statement on the completeness and consistency of formal systems. On a deeper level, however, there is an interesting commonality between the mathematics of incompleteness and startup disruption. It’s critical to understanding the dynamics how startups get born, get big or fail, and finally how the few survivors become legacy companies. Showing this deep connection between mathematics of incompleteness of formal systems and startups will be the purpose of this essay.

The Ultimate Theorem

“[My] own work no longer means much, I came to the Institute merely…to have the privilege of walking home with Gödel.”

Albert Einstein

It is surprising that Gödel’s famous theorem is all but unknown in the startup world. Thinking  of all the mathematical knowledge that has direct impact on computer science, software and startups I would be hard pressed to come up with anything more powerful than Gödel’s Incompleteness Theorem.

Y Combinator is famously named after Y Combinator, one of the best-known fixed-point combinators used to construct certain recursive functions. Yet who was the first to define and use a recursive functions? Gödel. Further, the proof that fixed points exist at all is a side effect implicit of his work. Y Combinator is direct descendant² of Gödel’s proof.

Consider another cornerstone of computer science, such as Alan Turing’s Halting Problem. He created that theorem when working at Princeton, right at the time when discussions about Gödel recent results dominated the institute mathematical debates. Turing’s proof is a continuation of Gödel’s work³. Kleene, Turing and Shannon were all standing on the shoulders of the giant – gnome sized Gödel – when they were following his groundbreaking proof and inventing modern computer science. We will review Halting Problem in more details later in this essay.

When you truly grasp the implications of what Gödel actually proved, it will be like opening a Pandora’s box  of wonderful insights. The implications of the theorem go far beyond just logic and math. Answers to the most sought after questions such as: Why can everything be made better? Why are so many startups possible and will always be possible? Why things we build tend to get more complex over time? Why does civilization always has room to improve?

To answers these questions, and  see how all these things are connected mathematically you need to understand Gödel incompleteness.

A taste of things to come

Naturally, there is a reason why Gödel theorem is still relatively unknown outside of mathematical circles. There are few big problems. First of all, Gödel’s proof is hard. Not “learn new computer language” hard, not “make an iPhone game” hard, really, really, really hard. Gödel did not make the task of understanding his theorems easy. Being famously introverted, he preferred the logic of his proofs to do all his speaking for him. Even mathematical education is not much help here. For example, Gödel offers the following preview, a “sketch proof”, what he called an “an intuition” for the real proof to follow.

We will define a class K of natural numbers as follows: K = { n ∈ IN | ¬ provable(R_n(n)) } (where provable(x) means x is a provable formula). K is the set of numbers n where the formula R_n(n) that you get when you insert n into its own formula R_n is improvable. Since all the concepts used for this definition are themselves definable in PM, so is the compound concept K, i.e. there is a class-sign S such that the formula S(n) states that n∈K. As a class-sign, S is identical with a specific R_q, i.e. we have S ⇔ R_q for a specific natural number q. We will now prove that the theorem R_q(q) is undecidable within PM. We can understand this by simply plugging in the definitions: R_q(q) ⇔ S(q) ⇔q ∈ K⇔ ¬(R_q(q)), in other words, R_q(q) states “I am improvable.“

Unless you are an active mathematician, reading and intuitively understanding his proof would be next to impossible. Just in case here is the proof again in case you enjoy sharpening your mathematical teeth against this amazing whetstone of logic⁴.

The second, even bigger problem is that understanding the proof will not help you much. Gödel’s logic is so alien, so strange that even understanding the formal deductions won’t help you understand all the implications of that phenomenon. Gödel’s proof is like a map with “X marks the spot”, yet on that map every border connecting it with our reality is torn away. You have no idea what particular area that map refers to. X is there, treasure is certainly there, but how the heck do you practically use it? In ironic self-referential self-validation Gödel’s formal proof cannot be understood formally. It requires an intuition leap that will unlock its secrets. And after you make that leap your perspective on everything related to startups and innovations will change. That is the insight we will try to develop⁵.

The Theorem

Gödel’s theorem is rapidly becoming accepted as being the fundamental contribution to the foundation of  mathematics – probably the most fundamental ever to be found.

            Roger Penrose

What exactly has Gödel proving? In modern language, simplified statement will be the following:

Any … formal system capable of expressing elementary arithmetic cannot be both consistent and complete. In particular, for any consistent, … formal system that proves certain basic arithmetic truths, there is an arithmetical statement that is true, but not provable in theory

Let’s work our way through that, since most of the concepts here are actually fairly easy to understand.

Formal systems are simple things. They are just collections of axioms and rules on how to manipulate them. For example, lets make a few axioms about numbers:

• The number 0 exists
• Each number has a successor that is a number. One follows zero, two follows one, etc.
• Two different numbers can not have the same successor
• … more axioms if you wish …

If we continue writing down such “self evident” axioms, we can arrive at certain set of axioms, called Peano axioms. These axioms and few rules of manipulations would constitute the simple arithmetic you learned in kindergarten if not earlier.

Axioms and rules about how axioms can be manipulated to produce derived statements is what constitute a formal system. Systems can be very different from each other. You can have just few rules about the numbers and stop at that – then you just get basic arithmetic. Or you can keep adding rules and axioms as long as they don’t make the system inconsistent. Gödel’s proof will apply to all systems that are complicated enough to include that kindergarten-level arithmetic. Most systems you encounter in real world and in your work will be much more complicated than arithmetic and thus fall under domain of Gödel’s proof.

Formal systems can be consistent or inconsistent. Inconsistent systems are practically useless, since in such a system anything can be proven about anything. In real world most of the formal systems you are dealing with are consistent or at least strive to be consistent. The consistency is important, since it means the system cannot at the same time prove mutually exclusive statements and therefore form contradictions. For example if my formal system deals with weather forecasting, it will be a sign of inconsistent system if it proves both “its going to rain tomorrow” and “its not going to rain tomorrow” at the same time⁶. Formal system can be constructed that give such contradictory predictions, but obviously its not going to be useful at all to us to actually predict is it going to rain tomorrow or not. If we construct a system that is consistent, then proving “it’s going to rain tomorrow” will also prove that “its NOT going to NOT rain tomorrow” – all deductions of such system will be consistent with each other⁷.

For example, how you make decisions about paid marketing campaigns in your startup? Well, you probably have few axioms (usually written on stone tablets by your CFO) and some rules how to interpret data from previous campaign: how to A|B test, how to make deductions based on that data, what to do next. The whole civilization we live in is full of systems that strive (with various degree of success) to be formal and consistent. Investment funds use complex financial trading systems, governments issue complicated regulations, the list of mankind attempts to formalize the universe around them is nearly endless: consider even the Bible with its famous ten axioms. Everything around you is collection of deductive rules and “self evident” axioms that remain largely unquestioned.

The premise of every formal system is that by using initial axioms of the system and using its deduction rules you will arrive to new true statements. You can then take these results, use rules and axioms on them again to arrive to yet more deductions. Your goal obviously will be to make a list of all true statements that can be deduced in the given system. If you want to create a formal system that is a new business model you incorporate axioms of arithmetic to describe how money works. Expanding your business model further, you will start deriving additional true statements like “User acquisition campaign will have positive arbitrage if lifetime value of average user is higher than average user acquisition cost”.

Finally, we would certainly want our system complete.  That means for every statement in the system you can either prove it or disprove it, and then keep the list of all true statements. Thus you would learn everything that there is possible to learn from given system. If your business plan includes an axiom “All actions should increase lifetime profit” you can then try to derive all true statementsabout how to make more money. Obviously we would want to get a complete system: if there are some ways to make money, we certainly would want to derive them from our axioms and know about them!

Yet look again at what Gödel has proven:

 “Any formal system capable of expressing elementary arithmetic cannot be both consistent and complete. In particular, for any consistent formal system, there is an statement that is true, but not provable in the theory”

That means that no matter how hard we try to derive all the results of a given theory, there will always be MORE true statements, more results that we  can’t reach within our formal system.  These statements, called Gödel statements or G-statements, will be out there, totally true and correct, floating in the abstract, yet totally improvable by deductions of our given formal theory.

Real world is far too messy and chaotic to resemble nice, clean logic of pure mathematical formal system. Yet we always have that optimistic hope that if we just work hard enough, if we are just diligent to account for all the details, if we do what it takes: get right education, find the right partners, use great methodology; and after all that great effort we can deterministically find next big breakthrough. We hope there is that one system we could use to mechanize our success in business or in life. Gödel demonstrated this to be completely false hope. No system will be ideal: even under best imaginable circumstances, when your industry can be reduced to pure mathematical formal system (which in reality is almost never possible), you still will be denied its full knowledge.The full implications of that result are staggering when you realize their full extent. Let me give you one quick example.

Imagine an Ultimate Monopolist, who wants to find all possible ways to extract money and value from the global marketplace and keep them inside his business empire. He is Bill Gates on steroids. What would be his “formal system” of economics & business? Whatever he wishes. Library of Congress? Done. Every single issue of the “Economist” since 2000 BC, clay tablet edition? Delivered to his office in gift-wrap. He can have formal systems as long and as expressive as he wants, and he is careful to avoid adding axioms that lead to contradictions. We will also throw in a full Google-plex or Gogolplex (your choice!) of computers to parse and analyze all that data, that will give him the list of all possible true statements derived from that system⁸: all the ways how to make money, create new profitable startups, all the ways to generate value.  Furthermore he has  money and manpower to immediately staff these startups and make them operational businesses. It’s a pretty cool gig to be an Ultimate Monopolist.

In other words our Ultimate Monopolist will stop at nothing to grab any promising business idea for himself, and throw his almost unlimited resources at the opportunity. That description is not far from reality when you think about modern Apple, Google, Facebook & Amazon.  These companies had built amazing semi-formal⁹ systems over the years and decades. Their systems are optimized for one thing – how to extract maximum value from marketplace of technology innovation. Their systems are immense – computer source code, marketing guidelines, “playbooks”, hiring guides and countless other printed and digital documents. That is the system their collective employees use in their daily work that’s how they train new ones. And on top of that, they have the tens of billions dollars in the bank necessary to bring about any conclusion of their semi-formal systems.

Yet despite all that might of formalized knowledge, again and again innovative startups appear out of nowhere. They constantly catch incumbents blindsided and make them pay billions to acquire the new discoveries. Be that Google or Facebook, anyone would love to jump on such ideas first and capture all the upside of new innovation for themselves, instead of paying billions to acquire a disruptive startup. So why can’t they? What is stopping trillion-dollar capitalization might of our technology cabal is the same: Gödel.

Gödel had proven that any kind of “Ultimate Monopolist” is still going to lose. There are true statements in his system – in other words there are new ideas and startup business models – that never can be proven in his formal system. No matter how many libraries of knowledge he will keep adding, how many more resources or computers he is going to add to his formal system of discovery, he still will never ever discovery every true statement (i.e. every profitable model) of his formal system of business. Ultimate Monopolist will always loose in the end because he cannot cover every statement, he cannot make his moneymaking empire complete.

A fork in the road

We are getting closer to answering the big questions posed at the beginning of this essay. We are almost ready to apply mathematical insights to our familiar world of startups, business models and innovation. However it would be a grave disservice to the amazing elegance of Gödel’s proof to omit the mathematical details. For those of you who would like to see the glimpse of the math involved I created the [special section] that includes a lightweight walkthrough. In that section we will also cover to basics of Turing Halting Problem and Cantor Diagonal Proof, which will be very important for us later. Feel free to read Gödel, Turing and Cantor: The Math first or just continue with our main narrative.

Formalization of Infinity

In mathematical section we just reviewed the technical details of the Gödel Incompleteness Theorem, the famous Cantor Diagonal proof and the Turing Halting Problem. Lets quickly recap what we learned for our readers who join us without reading up the mathematical details.

Cantor proof deals with nature of infinity. It shows that even between any two small real numbers, for example 1.1 and 1.2 there is an infinity so dense that even infinity of all natural numbers (which are numbers like 1, 2, 3, etc.) won’t be enough to count them all.  The infinity of real numbers, so called infinity of continuum is more “powerful” then an infinity of all countable natural numbers.

Gödel told us that no matter how long and complicated the formal systems we construct, there always will be true yet improvable statements. If we keep expanding our formal systems and make them bigger, that will only create more of such “true yet unprovable” Gödel statements.

Turing told us that you couldn’t capture infinite complexity with finite software code. Software itself cannot be bound or predicted by other software.  With very simple software you can create very complex behavior, and the only way to see the result of such complex behavior is to let such software run, which might require an infinite amount of time.

There is clearly something hiding behind all these proofs. Something so powerful that it keeps breaking the chains we are trying to put on it. Something out there is saying: You want to pick a few rules that will cover me in the net of deductions to know all about me? You can’t. You want to write software that will do all the hard work for you? You will never know if your software will ever finish working. And yet, what lies behind all these proofs is the true nature of continuum infinity. Infinity will always be far too rich, far too dense, far too big to be chained by anything countable – formal systems, software, and finite proofs. Better systems, better software can grab bigger chunks from infinity. Yet by expanding themselves they are no closer to fully capturing the potential variety hidden in continuum infinity. They just moved the boundary between “knowledge” and “unkown” further out.

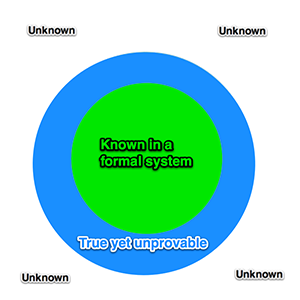
Lets try to understand what that means visually. Every system we use roughly will have three distinct areas. There will be an area of proven true statements, the “knowledge” of such system. This is what we can deduct in a given system, we can write it down and actually prove its true.

Then we will have an area full of true yet unprovable G-statements that belongs to that system. That is something that we can still express and write down in systems syntax, but we cannot prove. It may have a very clear pattern of actually being true like Goldbach’s conjecture yet we still are unable to write a hard proof.

And finally there is endless infinity of totally unknown space, that cannot be even expressed in a given system until more axioms are introduced.

That’s ok for first approximation, yet it misses a few important points. First of all – lets remember Cantor’s proof.  Even between real numbers like 1.1 and 1.2 there is an uncountable infinity of other numbers. Similar to that imagine that between any two points of our “knowledge space” or “idea-space” there might be infinity of new proofs and true deductions.

The system doesn’t represent one solid whole with sharp boundaries between known and unknown. It is more like a head of cheese riddled with holes, holes within the holes, etc. It is a much more complicated structure then what we can draw on paper. Formal system create certain grids over what we are trying to learn. Between the cells of that grid whole infinities might lie undiscovered. Each circle in our illustration should be riddled with infinity of small and large holes.

Finally, the biggest misrepresentation created by such picture is a sense of scale. The following would still massively overstate the coverage of our formal system against an infinity of unknown:

 Just like the following will overstate it again:

 Remember, this dot in the center will represent all the knowledge, all of the proofs of any given formal system. You can consider the biggest formal system of all – the totality of all recorded writings of human civilization since its inception. All that still will be just an infinitesimal dot comparing to the continuum infinity.

The World of Formality

The history of human civilization is a process of creation of formal systems serving a specific purpose¹⁰. From the earliest legal codes to modern data centers with terabytes of information we are trying to bring order and predictability to the chaos of infinite continuum. Creating formal systems is finding the balance between the “good enough” simplifications of infinite variety while preserving enough complexity of a given domain. The only way to go around our daily lives is to massively simplifying the world around us.  The rules, conventions, labels, best known practices, mental models and myriad other ways humanity has developed over the years solve the single purpose – chain the infinite complexity in some manageable, finite form we can deal with. Do something to create a practical shortcuts so that our simple brains can deal with that  finite, countable and limited model of reality rather then infinitely dense reality itself.

What Gödel, Cantor and Turing have proven so decisively is that no system will be ideal. All systems will be rough approximations that will never capture full variety of infinite possibilities of the continuum¹¹. There will always be gaps in our nets, imperfect labels, misinformation and missed knowledge just because we rely on the crutches of formal systems. The infinite reality of continuum doesn’t care where we draw our lines of given formalization. The very act of drawing lines will make certain knowledge hidden from us, the gist of Gödel’s proof.

The most brilliant minds already know pretty well about deficiency of any given formal system. The legendary Charlie Munger stresses the discipline of developing multiple overlapping mental models when developing his own formal system for investment. He understands no single system no matter how complex will give him the full truth¹⁶. But at least using multiple independent systems he can check if this or that idea is worth trying out. What is ambiguous within one mental model might be easily provable using deduction in another, and can be empirically verifiable in a third one. There is the risk of relying on formal system composed from other formal systems, yet Charlie greatly increases his predictive powers by knowing the limitations of each¹². That might explain why he is one of the richest people on the world.

Despite their limitations, we cannot get away from formal systems. Our brains can hold only simple, short & easily countable sets of axiom and rules, that’s how we operate. Yet the first step to avoid the worst mistakes is to be fully aware of natural limitations of formal systemss – that they are never full or nor complete model of reality they are trying to represent.

Now that we have better insight in interplay between formal systems we must use, and the infinite reality hidden behind them, we turn our attention to world of startups, innovations and the way our civilization propels itself forward.

4. The Unprovable Startup

Business Models

Every startup is formed with a dream to become a bigger company. As Steve Blank aptly put “A startup is an temporary organization formed to search for a repeatable and scalable business model”. And what happens after such scalable business model is found? What, fundamentally, is a company?

A company is a semi-formal system to extract money from the marketplace. Startups may skip the revenue-making part for a few years, but sooner or later what’s going to differentiate winners from losers is the ability to drive sustainable revenue from a business model they discover. To put things in perspective, here is one well known (at least among startups) example of the simplest formal business system.

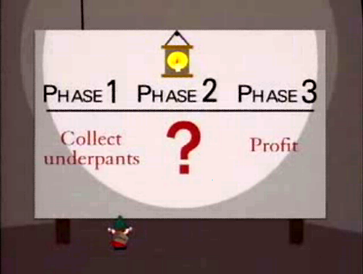As you can see, the system of South Park Gnomes consists of three rules. “Collect underpants” clearly implies a countable set of objects, meaning the system is compatible with Peano Axioms. That makes Gnomes business plan complex enough to “expressing elementary arithmetic” and it will be subject of Gödel theorem.

Next part of their system is “?”. That most likely is a free variable, the one that would accept a another system as its input. Gnomes is shrewdly using a meta-system so that they can change the specifics of business model depending on changing market conditions.

Finally, an axiom “Profits” which means the consistency of the system will be preserved if and only if all previous steps generate profit. A strong move obviously driven by Gnomes racial heritage.

If we remove Gnome specific “underpants” rules, the formal system of “? => Profits” would correctly describe pretty much every corporation in the planet. However corporations would need something more actionable then that.

Lets review that on few practical examples. To get things started lets look at Microsoft in the late 1990’s.

The Emperor of Redmond

By end of the millennium Microsoft was almost a monopoly over the technology field with unmatched power and influence. The rules and combined knowledge of that business empire would probably fill thousands and thousands pages. How you sell software to OEM partners? How you control pricing? How do you leverage strength in Office suite of products to keep competing operating systems out of the marketplace? How you leverage ubiquity of Windows installations to get favorable pricing from OEM partners? Myriad details, big and small.

The complexity of such formal system would be mind-boggling. At same time that system did require formalization. You need employee guidelines in every division. You need a system to train new employees. You need a system to pass knowledge when one executive replaces another. Over the years of transitions and employee rotations the intangibles will be lost, only formalized knowledge will be preserved. With tens of thousands of rules, Microsoft was in a unique position to extract amazing margins from its dominant positions in operating systems and office software.

Let’s imagine, for a second, a time traveler from the future appears in front of Bill Gates in 1999 and utters something like:

“I’m from the future! You should sell keywords to match search queries!”

What would Bill do with such a traveler? The syntax of his request is familiar – he knows what web search is and what keywords are. But everything else makes no sense whatsoever. There are few web search companies out there, AltaVista, Lycos. Their whole capitalization was less than Microsoft’s soda budget. They are troubled companies, far from being in great shape financially. Why on earth sell keywords for search?!

Bill can consult his experts, and dig into these thousands of documents on Microsoft servers representing their semi-formal system of value extraction. But there is very little there about search or keywords. The statement about selling keywords might be true yet having everything Bill has at his disposal, it’s utterly un-provable.

As an important side note, lets consider if time travelers move deeper into the past, to pitch Henry Ford or Nikola Tesla. However in this case the whole syntax of his proposition makes no sense. Computers do not exist, web and internet does not exist, everything he is saying is meaningless on a syntactical level. His statements belong to total unknowns for inventors of past centuries. Yet for Bill Gates, it represents a true yet un-provable statement.

Even if Microsoft knew in advance about keyword search, their formal system lacked any predictive powers to really evaluate that opportunity. Their systems were about software, OEM sales, computers and hardware. Google’s model just couldn’t be analyzed with it and therefore acted upon even with advance knowledge.

Thus it falls to Larry Page and Sergey Brin to formalize the system about web search and selling the keywords. The founders start with almost pure imagination, almost a dream:  to “organize the world’s information”. Since it turned turned out that such statement is very profitable one the cascading process of formalization of that domain rapidly followed. The new terms and axioms were added based on that purely empirical truth. The formal system of modern technological knowledge was expanded, and it generated its own new “true yet un-provable” massive opportunities. Nowadays when you call one of many Google satellite offices where hundreds of sales reps share with you thousands of tips and tricks how exactly to optimize search keyword campaigns for your small business you see directly the results of such formalization.

The Giant of Mountain View

Time passes. Our time traveler appears in front of Larry & Sergey in 2003 and utters the words of prophecy:

“I’m from the future! You should organize social friends graph between all people!”

Larry consults his formal system – it has thousands of documents about search engines, optimizations, ranking connections, etc. He can easily access public Microsoft servers and read about the smaller formal system of nineties  OEM sales, software, cutting oxygen supply to competitors. Unfortunately neither old systems nor newly expanded ones like the one Larry helped create has knowledge about building social graphs or maintaining friend connections. There are a few companies out there – Friendster and Myspace, their whole capitalization is less then Google’s sushi budget. Larry is perplexed – he understands the syntax of suggestion, but he totally lacks the tools to prove or disprove its profitability.

It falls to Mark Zuckerberg to formalize the system about building social graphs and optimal ways to extract value from it.

We can continue same narrative forever. Time traveler will appear to Mark, and give advice on say mobile photo-sharing. The formal system will be totally inadequate to prove the potential of the new idea. Only after somebody practically and decisively proves its potential by actually doing it, the previous un-provable model becomes part of the current business model.

The Magic Key

Successful startups:

• Discover new Gödel statements in a formal system of a given industry or marketplace.

• Build efficient expanded system to extract all value from newly discovered domain.

Failed startups:

• Build the model around unprovable yet false statement, or

• Discover a Gödel statement with very small potential, or

• Fail to build efficient system of value extraction thus letting others capture the new domain first

Successful huge startups are rare, unprovable, unique and disruptive. To be successful they must first discover new “true yet unprovable” idea in a system of a given industry or marketplace. This is very hard because these “Gödel statements” they need to find are so rare. After they find it, they must build a new, expanded formal system to extract all value from the domain they discovered.

Failed startups fail for myriad of different reasons, since the precious “true yet unprovable” statements are hidden amidst the infinite sea of false statements. They might build the model around unprovable yet false statement. That means even after years of efforts, there could be no profitable enterprise at the other end of the rainbow. Or they discover a Gödel statement with very small potential, which will be minimally working, but not well enough to feed and grow a VC-funded startup. And even if they succeed with all of the above, the formalization of new domain no one understood previously is no small achievement. Many startups may stumble on such a domain first (say Friendster) yet fail to build efficient formalization around it, thus letting others capture most value the new domain offers.

At each step of startup lifecycle there is different interplay between unpredictable complexity of the world and formalization effort to rein in and manage that complexity.

Inception: A tiny team of founders embark to test an idea. Rationally, it is impossible to prove such idea has big business potential. Yet we are human, and we are not perfectly rational. We are not robots that can only follow 100% logical deductions of existing formal systems. What will drive these founders might be an irrational intuition- passion about a specific domain, or just the desire to build things just because they like to build things. Existing formal systems with all their benefits and all their limitations are thrown overboard, and founders are largely free to do whatever they wish in totally unchartered waters.

Discovery: The product or service the team builds is released to the real world. Real world complexity is continuum infinity, it’s not bound by any formal systems. What market “wisdom”, startup mentors, university professors, and plain old “common sense” knows is irrelevant – that’s formalization of reality, not the reality itself. 

Usually the first product has next to zero probability to find the right spot for a new Gödel statement. Founders will be extraordinarily lucky even to land close enough to such statement on their intuition alone. Hitting exactly the right idea and right execution with all its myriads of tiny details is impossible. Continuum infinity of the real world demands an infinity of small details that needs to be adjusted to find exactly the right implementation.

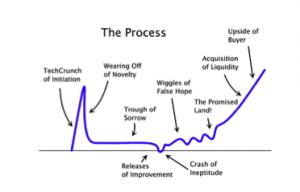
Startups can’t adjust infinite number of details at once. The only way they can proceed further is to maximize their discovery process if they work traditional “startup hours” to create maximum number of iterations possible in incredibly short timeframes. That process of frantic search generates the empirically observed startup curve. The iterations create the initial wiggles on the graph. If the startup zeroes in on the right point in idea-space of new Gödel statement they will move on to the growth phase. Otherwise they will die off as another failed startup in “false statements” area. The culture of fast iterations and pivots are natural consequence of free form search each startup runs in idea-space.

Unfortunately there are absolutely no solid predictions we can do about this stage. At the end of the day the startup just has to be lucky enough to start close enough and navigate optimally enough to hit its first discovery before company disintegrates from lack of funding or team morale. The process can be as fast as few months or as long as a decade.

Human patterns are playing huge role too at this stage. The “startup hours” and total lack of personal life is not easy on anyone involved. Startup is racing against complexity of continuum infinity while leveraging whatever formal system they have at their disposal. Increasing number of experiments, increasing speed of “experiment, feedback, next experiment” cycle greatly increases their probability of tuning all the dials to exactly the right value. It takes human leadership, human craftsmanship, team spirit to survive the rigors of this long process and to keep everyone motivated: that may sound trivial in the first month, but is an entirely different story by the 10^th month. Startups that can manage both sets of patterns: motivated, highly productive top quality team churning out experiments month after month while doing rigorous search process in idea-space without succumbing to infighting, demoralization, degradation of quality – would be the big winners of that phase. Everybody else would churn out and die as a failed startup.

Proof: Finally, if the biz model founders choose or pivoted into after many experiments represents a true statement of value¹⁷ extraction, they will immediately see explosive results that their model is working – very often much to founders surprise at the scale of their own success.

 Formalization: Now the startup’s challenge is to transition from early product, often held together by duct tape to professional system of extracting value from marketplace. We usually call that stage “explosive growth”. Startup goes into overdrive trying to both operate what they built and formalize the space it finds itself in. Be that Google ranking algorithms or pinboards¹⁸ at Pinterest, in every case the teams are working around the clock to understand better their new found domain, put software, processes, and training around all new discoveries, and explore new opportunities these effort brings. That is the most stressful yet incredibly exciting period for any startup.

Today creating software is one of the most powerful and scalable ways to formalize newly discovered domain. Software is eating the world is an unstoppable phenomena -because the human world is nothing more then a huge collection of formal systems. Software is the best tool so far to create most efficient and powerful formal systems for any purpose.

The process of formalization can take decades. As long as a startup has growth, especially non-linear growth driven by new products, the formalization is never finished. Yet sooner or later the process of formalization of any big discovery must end. Facebook will add the last unsigned user and will be permanently bound by birth rate. Everybody will own some version of the iPhone. Amazon’s catalog will carry every single item manufactured on the planet. The new expanded system that includes newly discovered true model might be big, yet it’s still a formal system, it’s still finite.

Sequential Gs: The greatest companies you hear about in the press are rarely single-G discovery products. To create truly massive company from a startup requires finding multiple independent Gödel-statements of increasing size. Perfect example of such would be Apple after Jobs return. Finding the company near bankruptcy, Jobs first bet was on relatively modest project of iMacs – a computer with focus on personal convenience and simplicity of use. That unquestionably was an idea from the domain of totally “unknown and unprovable” in the world dominated by the likes of Microsoft and Dell¹⁹. The success of iMacs created resources to find another unproven and unprecedented G-statement about music devices: the iPod. The success of iPods allowed for revolutionizing mobile phone business; and finally there was the breakthrough of formalizing whole new “unkown” domain of tablet computing.

This story is inspiring yet incredibly rare. Most startups would be lucky just to find one or two disruptive Gödel-statements to build their new business model around. Besides being lucky enough to find such sequential new models, the size of each new discovery must be much bigger to the previous one.

In the world of gaming, Zynga was a good example of relentless discovery of new disruptive properties. Starting few years ago from an online poker game, every year Zynga reached for new heights. Thanks to identifying and optimizing key new genre every year – such as Mafia Wars, Farmvile, and Citiville properties – it grew at unprecedented rate for the gaming industry. Every new genre it has discovered²⁰ led to bigger and bigger domains of value to be exploited every year.  Yet, since by the nature of the gaming business the staying power of these disruptions is much more limited then say Apple inventions, the demand for new discoveries is much higher. Now after suffering a catastrophic stock crash, Zynga is poised at yet another Gödel-test of its existence. Either they will find their next disruptive and unpredictable business model²¹ that will dwarf everything they have previously built, or their discovery will only yield a succession of false positives, and the slow transition into legacy company will settle in.

Legacy: If company stops innovating and loses capacity to proactively search for new Gödel statements first the non-linear explosive growth of formalizing new idea-space will slow down. Years later it will start bumping into objective limits of that new area that the startup discovered.

The process of formalization is complete. It brings its own unique benefits – new employees can be easily trained. The model can be transplanted to other countries with relatively little effort – unless cultures are radically different the formalization developed in birth country will be good enough as starting point in the rest of the world. The business becomes predictable and from the view of startup founders fairly boring.

At that stage startups resemble little of their wild beginnings. Making risky bets in early days would always pay off – it was rich undiscovered space ripe with possibility. The job of employees now is to simply execute the formal system developed during preceding years. Lack of risk-taking is not just driven by “big company bureaucracy” or lazy “9-5” corporate employees mindset. It’s driven because most of the potential and opportunities that were hidden undiscovered around original proof point, original Gödel statement that gave birth to the company are now tapped out²². The new expanded formal system is now well formalized and has little surprises left. New explosive discoveries can be made only by venturing far into unknown yet again. The big company can either try to facilitate that behavior (isolated labs, venture arms) or simply buy innovations via startup acquisitions.

The Company now becomes a permanent part of tech landscape. Its role is to continue operating the value extracting system and perhaps optimize a few things here and there to increase performance year after year. Apple was founded to upset IBM. Microsoft had stolen the personal computing torch from Apple. Google was formed to avoid the domain where Microsoft ruled supreme. Facebook leapfrogged Google’s dominance. And after all that cascading warfare you would expect just scorched earth and pile of bodies, yet what happens is exactly the opposite.IBM is still around, doing “ok”, and mind-blowingly is still selling mainframes! Microsoft still sells Windows and Office while tearing their hair out trying to find ways to be relevant. Tech companies rarely die unless extremely badly mismanaged, they just move deeper and deeper into legacy part of the stack, as new formal systems keep being added to the outer shell.

Now we have reviewed the major life cycles of startup, let’s run down key attributes of Gödel’s model and see what deductions we can come up with  for the startup domain.

90% of startups fail

Self evident from the nature of the startup space of ideas. The space of false statements is much larger than few points of undiscovered true statements. Every startup must go out there to total wilderness of not just unproven ideas, but ideas that cannot be proven in advance, and experiment based on blind faith to find such “true yet un-provable” ideas. Naturally most of such wild guesses would be wrong. In fact the 90% ratio was probably driven mostly by what used to be expensive and slow process of creating startups in the past. Right now the cost of starting a startup has collapsed to almost zero. Nowadays there are hundreds times more startups being incubated, while the relative density of Gödel-statements in the space have stayed the same. The failure ratio might become even more extreme like 99% or 99.9%. The fact that there are more startups doing experiments doesn’t change the extreme rarity of Gödel statements in the space of undiscovered business models.

Most startup ideas are bad

Closely correlated to the previous observation. Most of wild guesses about new Gödel-statement will be wrong. Very few will be extremely good. Paul Graham empirically classified these as “good ideas that look like bad ideas initially”. From Gödel’s model we can draw even more precise distinction. These ideas look “bad” because they are unprovable ideas in composite formal system “everything we know so far”. Bad ideas that are actually bad are usually provably bad even in current system. Discerning between the two is key skill for an investor and startup founder. If you start thinking about all the indicators of “provable bad” ideas, it will make it much easier to filter out the “unprovable” ones that you really ought to pay attention to.

When looking at new startups you should take special note when you hear something that is un-analytical, something that makes your mental gears skip turns since they suddenly lack axioms and rules to analyze the proposition. The usual reaction to that uncomfortable feeling is to think the idea is “bad”. Try instead what Gödel does in his proof. Can you prove that idea is bad? Can you prove the negation of the idea (anti-idea so to speak) is good? Can you use any of Charlie Munger style overlapping mental models to prove either? If your mind keeps drawing a blank no matter what approach you use it’s a strong indication you might be dealing with an unprovable statement in a given system. It doesn’t make it true, and is likely not true. Yet it certainly deserves a second look, you shouldn’t dismiss it just because its “unprovable” – it just might be a new Gödel statement. 

Startups are disruptive

Self evident from the nature of a given startup Gödel statement. Disruption means a totally unexpected way to do business in the marketplace – that is just a restatement that new startup business model is un-provable in the previous formal system. Disruption happens from the “truth” of newly discovered business models and its vast size makes it impossible to ignore.

Growth

Paul Graham also defined “Startup = Growth”. That is natural consequence of formalization of newly discovered domain. Startup initial product is never complex enough or extensive enough to cover all potential hiddens in the domain around newly discovered Gödel-statements of its product or business model. The initial Gödel statement is that swing of  pickaxe that sends the first gold nugget flying. All that potential is out there, surrounding initial point of contact, waiting to be formalized and therefore exploited. Growth means totally disproportional rewards for founder’s efforts. That disproportion happens because founders are mostly unlocking the value in domain they had found rather then directly creating value themselves. The formalization stage is a proactive exploration and mining of the new domain that the first strike located. The “gold” produced (might be revenue, might be users, might be investors) immediately goes back to powering even more effort to find the full extent of the newfound domain, increasing the extraction rate in the chain reaction. That leads to exponential growth Paul mentions in his empirical observations.

Competing directly with big legacy company

Obviously a bad idea. If you and your direct competitor are in same formal system, whoever formalized that system first got all the advantages. The business model is extracting value from marketplace, and they formalized far more efficient systems for far longer than small startup can afford or create²³. The new Gödel-statement is the one and only weapon startups have. It must leave the domain of the known and formalized to find its new domain of opportunity.

Startup strategies

Every few years we usually get a new popular strategy of incubating or running startups. Crossing the Chasm, Blue Ocean, The Four Steps to Epiphany and most recently Lean Startup. The books are good reads that will certainly help you. Yet it’s important to understand their intrinsic limitations. As we know new Gödel statements cannot be found by using any formal system. The strategies are valuable as long as they related to “human” patterns: “talk with your customers”. Yet all these systems become next to useless as soon as they delve into territory of mathematical reality of startup idea-space. When doing exactly the opposite of recent “Lean Startup” strategy led to the creation of newest multi-billion dollar company²⁴, is very telling example of the huge potential for misdirection these strategies contain. There were certainly some startups²⁵ that benefited from following Lean Startup or some other strategy. Yet the fact that some startups benefited from following it, and some benefited from following the opposite the opposite shows that startup success is independent from any such “startup system”. Obviously the danger is exactly the same to consider this essay some sort of “Gödel strategy” for startup incubation. Avoid the temptation.

The best approach to avoid these fallacies is to keep limitations of formal systems in your mind. No strategy will tell you which idea is good or bad. There is no software that will tell you if your idea is next billion dollar opportunity (HALT) or a fluke (loop forever): you must deploy the idea in the world to see if it “HALTs”. You cannot fake any part of that proof by using a system you picked up from the book. Therefore you have the right to override with your intuition everything and anything these systems tell you. As soon as these popular books leave the domain of human-related matters you are totally on your own.

Zombie startups

Most startups become so called “zombies”. They growth stops too early, and they have trouble realizing potential investors were hoping for. Yet they make some revenues, usually can keep few dozen people on staff, and continue doing what they are doing for many years. “Second Life” would be a good example of startup that seemed to have huge potential early on as new social platform yet ended up with relatively small user base and was driven to near-irrelevance by the rise of Facebook. 

Zombie startups represent small Gödel-statements. They are the small dots in the 3-area chart we used above. Gödel’s theorem only proves they exist – it doesn’t prove anything about their size or distribution. There will be Gödel statement for $100 opportunities just like there would be a few for $1B ones. Zombie startups unfortunately have stumbled upon such a statement that does generate revenue or users, yet the limit of that newly discovered domain is far too small. Instead of having decades to grow into that newfound space, startup hits the walls far too early and is now limited to much smaller revenue streams and overall potential.

The best advice to give to startups that find itself in such situation is to treat early product as source of free cashflow and find a way to aggressively experiment in surrounding areas to find new Gödel statement of much higher volume.

M&A, pre-traction

Why are some startups bought pre-product, pre-traction? At that stage it’s purely domain of “human” patterns. The team background, simple charisma of team leader, the desire to invigorate a stale corporate workforce, or myriad other reasons may lead to a vote for or against such deal. From perspective of formal analysis there is no hard data yet to make any sort of conclusion.

M&A, early traction

That the type of deal most corporate development officers are looking for, especially if they can get the team at relatively low price comparing the the future value of the domain they are actively unlocking. Now everybody sees hard proof that new model is actually working, the only risk remaining is what is the ultimate size and potential of such domain? Instagram purchase by Facebook falls exactly into this category of deals. Where would Instagram growth stop if it was left to fare on its own: $10B, $100B? We will never know since now all the benefits of formalizing this new domain of picture-driven social experience will belong to Facebook.

M&A, post traction

Its often puzzling to the newcomers to the tech industry why some companies like Instagram can get a x1000 multiplier of their revenues in deal valuation, while another company with huge revenue stream will get x3-x5 at best? The reason is company position on the timeline of unlocking all the potential from the new domain. As your startup starts to accumulate years of operational history, these years will serve as an indirect indicator of your startup future potential. Everybody will assume if you generated certain revenue  after operating for say 5 years, it’s very unlikely you will generate ten times bigger revenue in year 6. Such statement would be incorrect for any pre-traction and early-traction startups.  They are exactly in the ground zero of Gödel-disruption – for them everything is potentially possible. Yet that is no longer true for a startup who is past formalization stage of a new domain. As years pass corporate officers will assume whatever potential for disruption it had its now behind it, and a startup is bound by the gravity again. Their growth becomes more predictable, more linear, big surprises are becoming almost impossible. Since its future upside potential is now limited, it is reflected in valuation multiplier. 

These are the first few observations we can make from applying Gödel Incompleteness model to the domain of startups. As you consider all phenomena you encounter in startup world our new formal system is there to help your mental modeling. As we know all too well now our list of deductions about startups will always be incomplete. Yet even if goal of completeness will be forever out of our reach, let’s try to make that list as comprehensive as we can. Ask all the questions you want to be reviewed from Gödel perspective in the comments, or add your own analytical observations! I will be updating this essay with your best contributions.

Black Swans

It’s impossible to write about Gödel Incompleteness without mentioning Black Swan book that achieved a cult following in Silicon Valley since its release in 2006. The book is incredibly deep and it will be a disservice to simplify all its ideas for the purpose of a blog post. Therefore we will address this part to the readers who already are very familiar with the book and we will direct others to experience it first hand.

In our terminology Black Swan events would be instantiation of Gödel-statements in any existing social or economical system. The original book deals mostly with negative Black Swans – undecidable statements inherent in the system that satisfies the attribute of system collapse. The positive Black Swans are mentioned exactly in the context of the startup world. In this essay we have concentrated on such positive Black Swan events that led to value creation provided by startups. Over time these positive Black Swans lead to the progress of civilization: ongoing process of formalization of larger and larger domain of continuum infinity.

The source of negative Black Swans that can topple financial systems, countries, and governments is exactly the same as the source of positive Black Swans that lead to growth, new opportunities and progress. The source is Gödel Incompleteness.  Every formal system by virtue of existing will contain both the seeds of its own potential destruction and seeds of its own possibilities of expansion. Both of these will be unprovable and therefore unpredictable. There is a very deep connection between Black Swan events and Gödel statements.

Epilogue

Disruptive startups springing into existence out of nowhere might look like random positive Black Swans. Yet what makes their formation not only possible, yet outright inevitable, are fundamental dynamics similar to Gödel Incompleteness. Just like strict formal systems of pure math will always contain proof of their own incompleteness, so the very act of formalization of reality undertaken by big established corporations will always contain within itself the seeds of its future disruption: true yet currently unprovable statements of the successful startups of the future. Every startup will start in a totally unprovable, unpredictable new domain they can discover only empirically, by building and launching something with no assurances of success.

It’s inspiring to know at any moment in time there is an infinite number of true statements for new startups to discover and further expand our collective system. Gödel’s theorem is not really about our limits: it’s about possibilities always waiting to be discovered. The process is certainly hard and alien to us. Out there, outside the comforts of the “known” there will be no formal systems to help us as we grow so accustomed to throughout our lives. All systems of meaning, convenient assumptions and well known predictions will be rendered useless. New startup cannot be invented in the library of our past knowledge and existing systems. It will always require an intuitive leap of faith or passion to cross the chasm of unknown and unprovable. Yet, as we know, every year dozens of startups and their triumphant teams cross that chasm to start formalizing domains previously unreachable to human thought and ingenuity. The mathematical reality of these domains ensures that this process will never stop; the expansion of our formalized knowledge will never cease. The human intuition unbound by limitations of pure formality will always push forward, find new domains, and leverage the amazing powers of software formalization to bring the fruits of new knowledge to the rest of the civilization. Your intuition just like your powers of formal deduction is all you need to join in.

Credits

Big huge thanks to the amazing team of reviewers who helped so much to improve this essay. Author is indebted to Elliott Wolf, Jeremy Carr, Igor Shoifot, Kamal Ravikant and  Tim Hanson for reviewing this text and contributing a number of valuable suggestions. Doug Lee as always provided a number  of great design insights. It’s impossible to overstate the effort of my editor Laura Ochoa, who was tirelessly reviewing draft after draft of these writings.

Research Resources

• Gödel proof translation in modern language: http://www.research.ibm.com/people/h/hirzel/papers/canon00-goedel.pdf
• Older Gödel proof translation: http://jacqkrol.x10.mx/assets/articles/godel-1931.pdf
• Recursion: http://www.people.cs.uchicago.edu/~soare/History/compute.pdf
• Charlie Munger network of mental models for investment: http://www.focusinvestor.com/FocusSeriesPart3.pdf

Wikipedia entries

• http://en.wikipedia.org/wiki/G%C3%B6del’s_incompleteness_theorems
• http://en.wikipedia.org/wiki/G%C3%B6del_number
• http://en.wikipedia.org/wiki/Fundamental_theorem_of_arithmetic
• http://en.wikipedia.org/wiki/Diagonal_lemma
• http://en.wikipedia.org/wiki/Halting_problem
• http://en.wikipedia.org/wiki/Diagonal_proof
• http://en.wikipedia.org/wiki/Fixed-point_combinator
• http://en.wikipedia.org/wiki/Unsolved_problems_in_mathematics
• http://en.wikipedia.org/wiki/Continuum_hypothesis#Impossibility_of_proof_and_disproof_in_ZFC

---